You can (obviously) create 3D graphics with only easy-to-understand trigonometry and no abstract and hard-to-understand matrix math, but I've never seen anyone talk about it. Until now! The following method limits rotations to the Y axis only, which means you can rotate to the left and right but you can't look up and down (if that was enough for DOOM, maybe it could be enough for you as well?) I've done this in pure WebGL shaders, but you can probably use the math in other frameworks as well. I just mention it in case any of the code happens to be specific to WebGL.
You basically do the following steps, for every point in every triangle that together make up the three-dimensional objects in the game world, to convert their 3D coordinates to two-dimensional coordinates onto the actual screen. In this example, we know the xyz coordinates for the point, the xyz coordinates for the camera, and also the camera's rotation (the angle/direction it looks toward), which you normally know when programming a game.
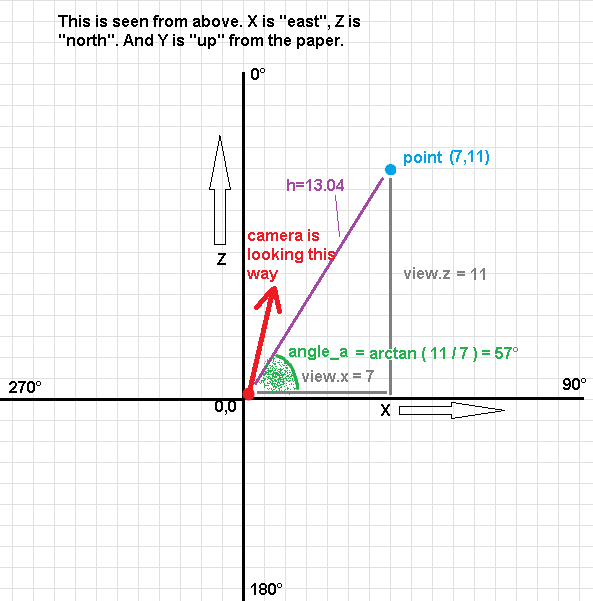
In a DOOM like rendering where the camera only rotates around its Y axis, the height on screen for a point is simply the height of that point in the world divided by how far away it is from the camera. No more trigonometry than that for the height. So we can focus on just X and Z, and visualize the coordinate system on a paper as if it was seen from above.
First we want to adjust the world's coordinate system to the camera, so we subtract the point's X coordinate by the camera's X coordinate, and the point's Z coordinate by the camera's Z. Mathematically we actually move the whole world to the camera and not the other way, so the camera gets the coordinates (0,0) to make calculations easy. It doesn't matter to the viewer if we move the world or the camera, because it will look the same. This gives us the "view coordinates":
view.x = point.x - camera.x; view.z = point.z - camera.z;
The left image shows the point and camera coordinates in the world, the right image shows their "view" coordinates after we've done recently mentioned procedure:
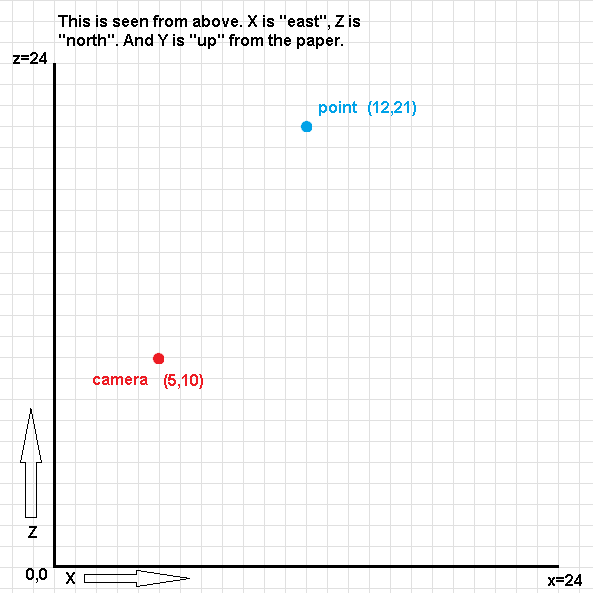
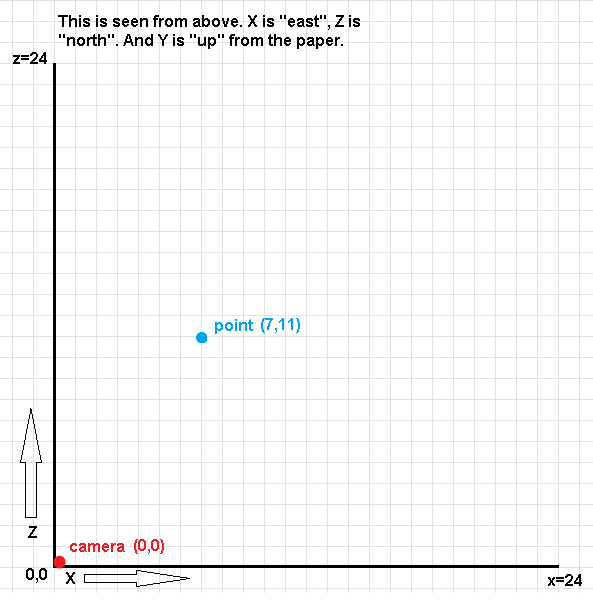
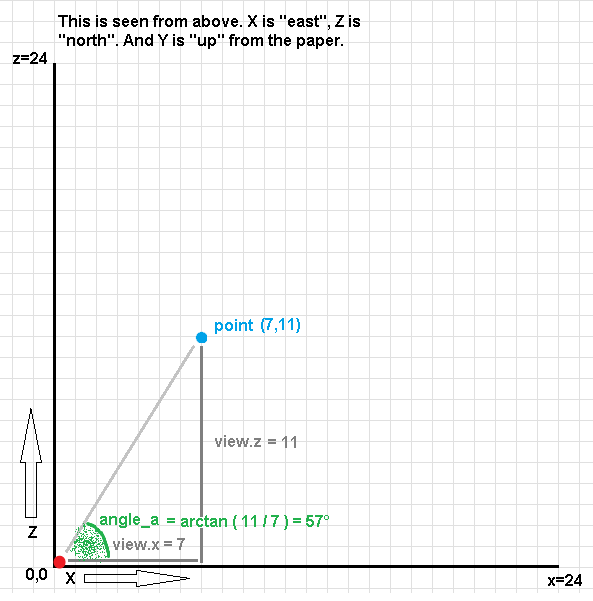
After adjusting the point's position to the camera, we also want to rotate the whole world according to the camera's rotation for the same reason. We do some trigonometry magic to get some triangles, angles and a hypotenuse for this to work. This is pretty straightforward to visualize on paper (not easy, but straightforward). In the end we get the "rotated coordinates":
angle_a = atan ( view.x / view.z );
angle_b = camera.rotation.y - angle_a;
if (view.z < 0.0) angle_b += 3.14; // this is done to not draw things that are behind you.
// atan() will give the same values for both positive and negative angles, I think
hypotenuse = sqrt ( view.x*view.x + view.z*view.z );
rotated.x = -hypotenuse * sin (angle_b);
rotated.z = hypotenuse * cos (angle_b);
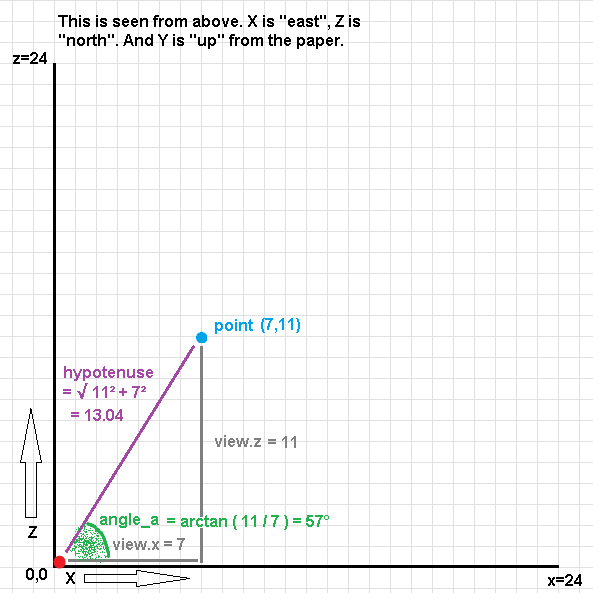
Now we have adjusted the world to the camera, but we're still in a three-dimensional world. To get the two-dimensional screen coordinates for the point, we divide the X coordinate with the Z coordinate (the depth) - if a point is to the right side of you, it will be on the right side of the screen, but if it's further away from you it will be LESS to the right. That's just how perspective works. And the screen Y coordinate is calculated as described earlier, by dividing the height difference between point and camera with the recently created Z coordinate, to create perspective in the same way. This gives us the "projected coordinates":
projected.x = rotated.x / rotated.z; projected.y = view.y / rotated.z;
Calculating your own 3D rendering doesn't have to be more complicated than this. It's not super easy, but there are few steps and only triangles and trigonometry that you can draw on a paper to understand every step. You never have to go into abstract land and accept how you won't understand everything. Here you can understand everything! To me, understanding what happens in my code so that I can freely change, remove or improve anything without friction, is often more important than code size, code speed or code "readability" (or depending on which camp you're in, avoiding abstractions and exposing the truth underneath IS readability).
SUMMARIZED: Adjust the coordinate system (both position and rotation) to the camera, to get how far away the point is from you (the camera) in depth (Z), vertically (Y) and to the left/right (X). Then project this to a 2D screen by using perspective (screen Y = height divided by depth, screen X = left/right divided by depth) to make things further away smaller and things closer to you bigger.
kbrecordzz, 2025
(backstory)
3 years ago I sat down to learn how 3D graphics actually works, and none of the examples online explained how 3D calculations works, just how to use them. They showed how you create 3D with the help of "matrices", but no one explained what matrices are and how they work (I'm starting to realize that maybe no one understands them intuitively, only practically). In my head, a compelling 3D rendering should be possible to create by rotating and moving coordinates and then calculating the perspective to make things closer bigger and things further away smaller. And this should be able to do with trigonometry. I never understood why all the four-dimensional arrays? I drew sketches to visualize it, and made a small C program to output a small 3D world into the terminal, but it never worked perfectly (probably because I didn't realize I was drawing things both in front of and behind me). Then the idea lied in the back of my head for years, and my failed experiments made me doubt my ideas. "Maybe there's a reason people use matrices", since I didn't get my trigonometry 3D to work. But, 3 years and lots of knowledge later, I got it to work! So, your intuition can be right even if all written evidence don't confirm it. But please don't forget how many times you're wrong too.